本文是GPU并行程序优化系列的第三部分,以矩阵转置为例,挖掘其在GPU上程序的进一步优化。之前关于本例的初步优化请参见“GPU程序优化(二)”一文。建议有一定的CUDA编程基础,再来阅读文本。
Catalog
已经达到极限了?
经过了对行、各元素并行化处理,OK,似乎目前得到了一个还不错的结果,难道就这样结束了吗?这个时间是GPU上的最快速度吗?
当然不是了,请继续本文的学习。
影响代码性能的两个主要方面
首先,2件事情会限制任何代码的性能:
- 对内存的读取/存储所花费的时间;
- 对该数据执行计算操作花费的时间。
反观目前的转置代码,已几乎没有计算部分了,完全是关于数据移动。那么计算就可能不是瓶颈所在,应该关注内存方面的瓶颈。
小提示,要看移动数据是否有效率,有个方便的程序——device Query,包含在CUDA SDK里,可查询大量设备信息。
优化代码内存操作
看代码内存操作是否有效——DRAM utilization
下面的几个参数是我们能通过device Query查询得到的,也是计算内存读取相关参数的依据:
- GPU clock rate (GHz)——每秒GPU周期clocks/second
- Memory clock rate (MHz)——每秒内存周期clocks/second
- Memory Bus Width (bit)——每时钟周期传输的比特数bits/clock
是目前要关心的几个信息,从中可得到:内存读取的最大速度,也可以理解为内存峰值带宽(Theoretical peak bandwidth)。
以一组数据为例,假设从Device Query中查询到:
- Memory clock rate: 2508 MHz
- Memory bus width: 128 bits
则理论上的内存峰值带宽是上述两者相乘,得40.128GB/s.
一条经验法则是,如果实际内存带宽:
- 达到理论内存带宽的40%~60% -> okay;
- 达到理论内存带宽的60%~75% -> good;
- 达到理论内存带宽的75% -> excellent。
实际上,真正的代码会有额外开销,永远无法达到此理论峰值带宽。
那么本代码中我们的实际内存带宽表现如何呢?
实际Kernel达到的带宽(假设运行时间为0.67ms,N = 1024):1024*1024*4(4字节数据)*2(2次读写内存)/0.67e-3 = 12.5GB/s。可以看到,与40.128GB/s上相比,效果并不是很好。
| Code version | Time | real BW | DRAM utilization |
|---|---|---|---|
| serial | 466ms | 0.018GB/s | < 0.1% |
| parallel per row | 4.7ms | 1.8GB/s | 4.5% |
| parallel per element | 0.67ms | 12.5GB/s | 31.1% |
那么为什么并行化到元素级别后,DRAM利用率还是这么低呢?
coalesce合并
下面来思考一下可能的解决办法。一般来说,会想到coalesce合并。
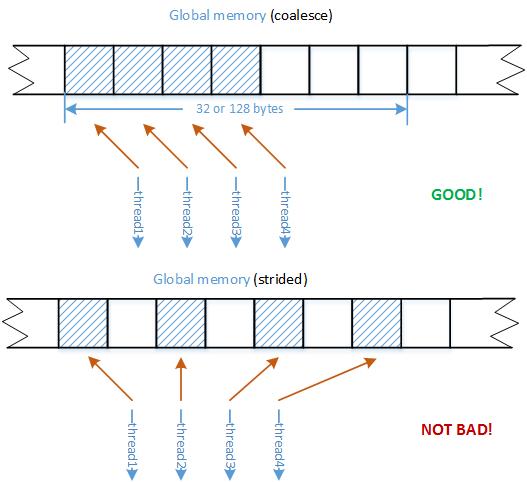
GPU始终访问全局内存中较大的数据块,以32个或128个字节访问DRAM。这意味着,如果warp中的线程访问连续相邻位置的内存数据,将会使读的效率有所提升。相反地,如果一个warp中的线程读取或写入完全随机的地址和内存,肯定会得到较差的合并效果。所以,更为常见的折中访问方法,称为跨步strided,访问的内存位置是它们的线程标识与一定步长乘积的函数。以图为例,这种隔一个读取的方式,相比于紧相邻的访问方式,只增加了一倍的内存事物,但相比于完全随机的大跨步的访问,效果自然好很多。
所以依照coalesce的思路,我们的代码肯定还有可优化之处。
可以看到代码中的N就是跨步,目前是1024。i的读取是相邻的,这是我们想要的,是好的合并,但同时,写入输出矩阵时,却是以N = 1024为大跨步的访问方式,这显然很不好。因此我们找到了问题的根源!
因此我们的问题是实现了合并读取,却是分散写入。而解决问题的目标是合并读取,合并写入。
解决策略:
每次取输入矩阵的一个图块,把它转置并复制到输出矩阵内对应的转置后的位置。这是一个单线程块的工作,所以此线程块中的线程要一起合作执行复制并同时转置元素图块。
线程块中的线程将该图块复制到共享内存,在其中执行转置。如果图块足够大,假设K=32,K*K大小的图块,每个warp线程组每次将复制32个元素到共享内存,由于对warp中的32个线程在内存中相邻的位置读取、写入,将会得到还不错的合并。然后再把转置的矩阵以合并的方式复制到其全局内存中的新位置,即可完成。那编程测试一下吧!
const int N = 1024;
const int K = 32;
__global__ void transpose_parallel_per_element_tiled(float in[], float out[])
{
int in_corner_i = blockIdx.x * K, in_corner_j = blockIdx.y * K;
int out_corner_i = blockIdx.y * K, out_corner_j = blockIdx.x * K;
int x = threadIdx.x, y = threadIdx.y;
__shared__ float tile[K][K];
tile[y][x] = in[(in_corner_i + x) + (in_corner_j + y) * N];
__syncthreads();
out[(out_corner_i + x) + (out_corner_j + y) * N] = title[x][y];
}
为了节省额外的同步线程,将从in中读取的数据以转置的形式存入共享内存([y][x]),同步后,再以合并的方式写入全局内存。 因为如果将in的图片块读取到共享内存需要一次同步线程,执行转置后也需要一次。
优化到这里还没有结束。实际运行后用NVVP检查效果,发现global load/store efficiency 都为100%,但是DRAM utilization 很低。注意到Shared memory replay overhead却比较高。
从little’s Law中找继续优化的方法
先回顾一下优化时关注内存的原因——使用GPU加速代码运行。而GPU之所以具备这样的能力有以下原因:
- 大规模并行,单个芯片上有成百上千的处理器;
- 高带宽内存系统。
因此如果内存系统不能有效将数据传递到这些处理器中,并及时存储结果,那GPU工作的效率就是打折扣。因此对于一个内存受限的kernel函数,存在一个优化的子目标——充分利用可用的内存带宽,这也是我们注意coalesce合并、DRAM利用率的出发点。
那什么是可用的内存带宽?——排队论中的Little’s Law说明了这个问题。
Number of useful bytes delivered = average latency of each transaction * bandwidth 传送的字节数为每个内存事务的平均延迟与带宽。
鉴于此,得到了改善代码的方法可以有以下出发点:
- 增加传送的字节数;
- 减少事务间的延迟可以提升带宽。
如果将这一现象比喻做顾客在星巴克排队买咖啡,那么增加传送的字节数,就是有很多服务员同时提供咖啡,减少事务间的延迟则是需要服务员更快地提供服务。
GPU的Little’s law就是在GPU中把一块数据从SM移动到DRAM中,或从DRAM获取信息转移至SM,类似的DRAM操作事务将耗费上百个时间周期。这表明试图读写全局内存的线程得耗费上百多个时钟周期用在等待数据上,而这些时间本可以更有效地利用。
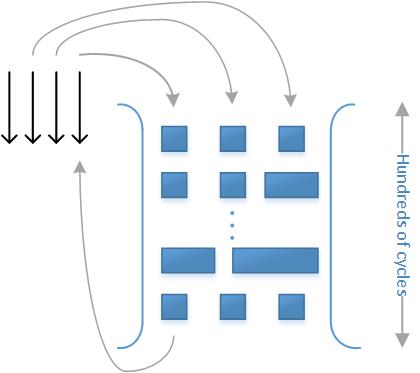
可以把内存系统看做一个很深的管道,线程发出请求让内存事务填满管道,比如是load或store指令。结果是事务落入管道底部,又返回至线程。一个事务通常需要200到300个时钟周期通过这个管道,同时能容纳大量的事务。可能会发生这种情况,只有几个线程发出事务,或各事务间延迟太大,管道几乎为空,只能传递少数字节,根据little’s law,带宽会受损。 但是若不容易让内存事务更加“宽阔”,则可以尝试让事务更多。
我们的程序是分配给每个元素一个线程,因此在事务数量上不存在太大的问题。那会是平均延迟的问题吗?
仔细检查代码发现,__syncthreads()似乎就是症结所在。 32*32=1024个线程都做很少的工作,然后再barrier处等待,直到其他线程均完成。在线程块中的线程越多,花费在等待上的平均时间越多。这无疑增加了平均延迟。
有什么方法可以减少平均延迟时间?
- 减少每个线程块中的线程数;
- 增加每个SM中的线程块数。
根据减少平均延迟的方法,不妨可以尝试减少一个线程块中的线程数。把K = 32改为16得到的结果显示确实更好了些。感兴趣的话可以尝试K = 8等。
| Code version | Time |
|---|---|
| serial | 466ms |
| parallel per row | 4.7ms |
| parallel per element | 0.67ms |
| tiled (K = 16) | 0.52ms |
SM中的occupancy占用率
什么限制了一个SM中线程块的数量?先看看占用率occupancy。每个SM中的下列资源数量是有限的:
- 线程块数,如8;
- 每个线程块中的线程数,如1536/2048;
- 用于所以线程的寄存器数,如65536;
- 共享内存字节数,如16K-48K;
用CUDA SDK调用device Query能方便采集上述信息。通过它们可以计算每个SM上运行的线程数量,也可以得到限制性能的主要矛盾。
在我们的例子中,kernel要求1024个线程,而一个SM支持最多2048个,也就是本例仅使用了一个SM中的2个线程块,而限制了使用更多(最多8个)。这里注意occupancy是和GPU平台强相关的,换一个平台上述信息得重新获得和评估。下表给出了程本序在多个平台下的occupancy示例:
| Platform | max threads running | max threads possible | occupancy |
|---|---|---|---|
| Laptop | 2048 | 2048 | 100% |
| Fermi | 1024 | 1536 | 66% |
改变kernel函数 occupancy的方法:
- 控制一个线程块需要的共享内存(修改图块大小);
- 修改启动kernel时的线程(块)数量;
- 用编译器控制内核使用的寄存器数量。
提升occupancy会一定程度上提升,但可能也会使GPU运行效率降低,这是个权衡问题。比如减少图块大小也会使得有更多的线程块运行,但图块太小就失去了划分图块存取的意义——保证coalesce合并访问全局内存。
优化代码计算性能
前面关注于优化内存访问(通常是GPU优化的瓶颈), 另一方面,优化计算性能也很重要,归结为两个方面:
- 最小化在barrier处等待时间;
- 最小化线程发散度。
其实关于第一点的处理方法在前文中已经说明了,那么重点关注如何减小线程发散度 (thread divergence)。
减小线程发散度
首先要明确warp的概念:一组操作步调一致的线程,无论数据类型,都用同种指令执行。更为通用的叫法就是SIMD,类似的术语还有SIMT,单指令多线程。
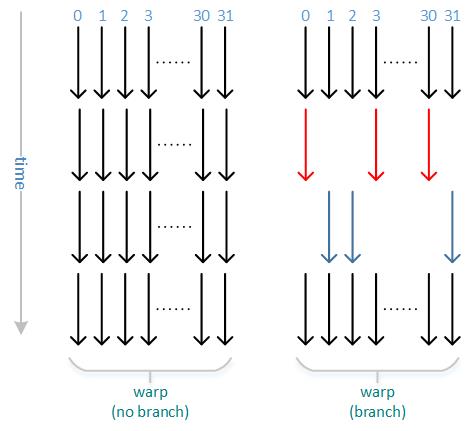
若非分支操作,各线程在时间维度上在一组warp中整齐排列;而对于分支操作,一组warp中部分线程执行if分支,另一部分执行else分支,如图所示就将并行度打破,使时间拉长,存在一些线程空闲而另一些线程在执行的浪费,这就叫做线程发散。若无嵌套的if,else,称为2路发散,否则有4路、8路等,会花更长时间。
对于一个包含1024个线程的线程块,最大的线程分散penalty是多少?答案是32倍的时间浪费。原因是一个warp只有32个线程,在这种最坏的情况下,一个线程执行一个分支。比如switch中带有大于等于32个case的情况。
减小分支分散需要从算法设计上改进,有几个原则可以注意:
- 尽量避免分支代码,避免使相邻线程采用大量不同分支;
- 尽量避免线程工作量间的不平衡,小心使用循环、递归这类代码。
选择效率更高的数学计算——提升“最后一点性能”
这些trick用来提升最后一点性能:
- 只在有需要时才用双精度运算,如
float a = b + 2.5就没有float a = b + 2.5f性能好,因为GPU中2.5默认为双精度,但这里仅需要2.5f就可以。 - 可以使用内部函数 (intrinsic functions),如__sin(), __cos(), __exp(),都为单精度输入输出,可能精度比math.h低,但快很多。